前序遍历 #

假设我们有以下二叉树

     1
   /   \
  2     3
 / \   / \
4   5 6   7

对这棵树进行前序遍历的访问顺序为：1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7。

具体实现的过程如下：

1. 从根节点 1 开始遍历，访问它，输出 1。
2. 接着遍历左子树，先访问节点 2，输出 2。
3. 继续遍历 2 的左子树，访问节点 4，输出 4。由于节点 4 没有左右子树，返回到节点 2。
4. 访问节点 2 的右子树，访问节点 5，输出 5。节点 5 没有左右子树，返回到节点 2。
5. 返回到节点 1，访问 1 的右子树，访问节点 3，输出 3。
6. 继续遍历 3 的左子树，访问节点 6，输出 6。节点 6 没有左右子树，返回到节点 3。
7. 访问节点 3 的右子树，访问节点 7，输出 7。节点 7 没有左右子树，返回到节点 3。
8. 遍历完成，输出的结果即为 1 2 4 5 3 6 7。

代码实现（1） #

var res = [];

// 返回前序遍历结果
function preorderTraverse(root) {
  traverse(root);
  return res;
}

// 二叉树遍历函数
function traverse(root) {
  if (root === null) {
    return;
  }
  // 前序位置
  res.push(root.val);
  traverse(root.left);
  traverse(root.right);
}

但你是否能够用「分解问题」的思路，来计算前序遍历的结果？

换句话说，不要用像 traverse 这样的辅助函数和任何外部变量，单纯用题目给的 preorderTraverse 函数递归解题，你会不会？

我们知道前序遍历的特点是，根节点的值排在首位，接着是左子树的前序遍历结果，最后是右子树的前序遍历结果：

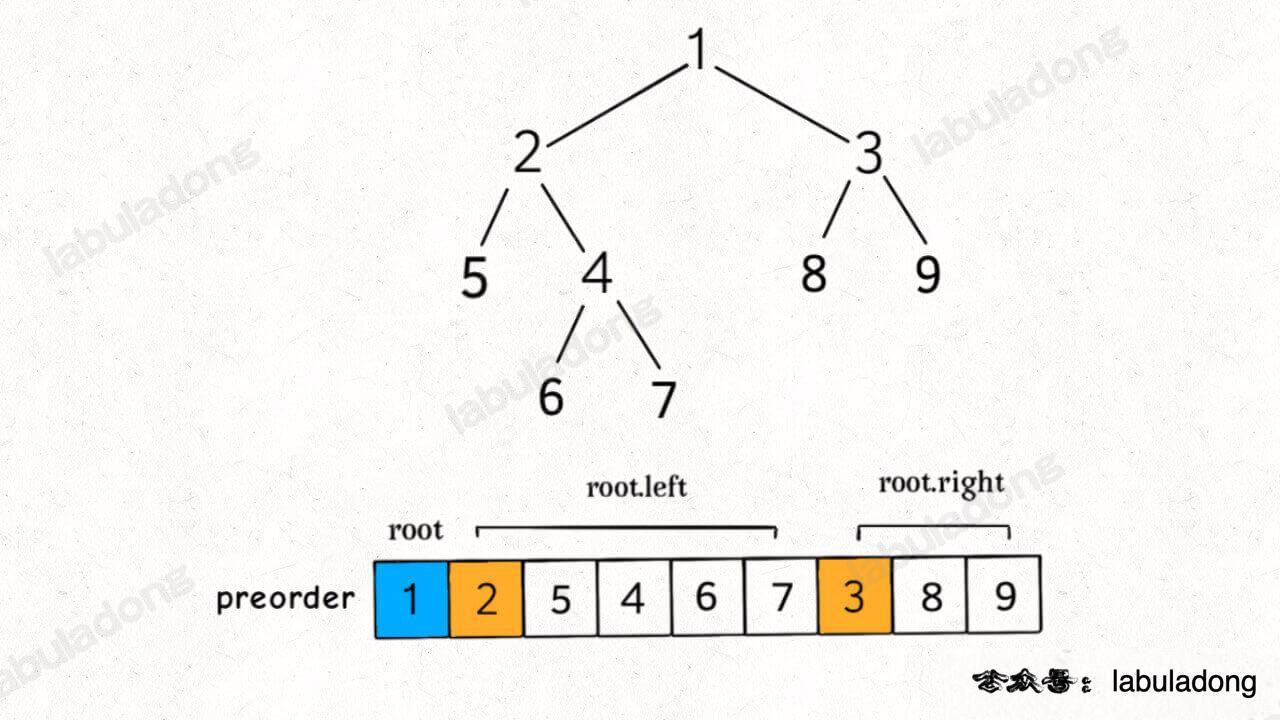
一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果。

所以，你可以这样实现前序遍历算法：

代码实现（优质不占用空间） #

// 定义：输入一棵二叉树的根节点，返回这棵树的前序遍历结果
function preorderTraverse(root) {
  var res = [];
  if (root == null) {
    return res;
  }
  // 前序遍历的结果，root.val 在第一个
  res.push(root.val);
  // 利用函数定义，后面接着左子树的前序遍历结果
  res.push(...preorderTraverse(root.left));
  // 利用函数定义，最后接着右子树的前序遍历结果
  res.push(...preorderTraverse(root.right));
  return res;
}

中序遍历和后续 #

中序和后序遍历也是类似的，只要把 add(root.val) 放到中序和后序对应的位置就行了。

总结 #

综上，遇到一道二叉树的题目时的通用思考过程是：

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。

3、无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。